Question

Let H = (R+, x) be the group consisting of the set of all strictly positive real numbers with the binary operation given by multiplication. Show that H is isomorphic to (R, +), the group consisting of all real numbers with the binary operation given by addition.

Answer 1

Answer with Step-by-step explanation:

We are given that a group H=
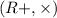`(R+,*)` b consisting of the set of all strictly positive real numbers with binary operation given by multiplication.

We have to show that H is isomorphic to (R,+) where (R,+) is a group consisting of real numbers with binary operation given by addition.

Isomorphic group :If there is one-one correspondence between the elements of two group with respect to given binary operations and there exist an isomorphism between two groups then the groups are called isomorphic groups.

Suppose a function

f:
`(R+,* )\rightarrow (R,+)`

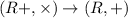
f(x\cdot y)=f(x)+f(y)

If two groups have same order and have same order elements then we also says that the groups are isomorphic.

Order of H is infinite and order of (R,+) is also infinite.

H have one element of order 1 and one subgroup of order of order 1 and (R,+) have one element of order 1 and one subgroup of order 1.

(R,+) is infinitely generated and and H is also infinitely generated group.

Both have same properties .Hence , H and (R,+) are isomorphic group.