Question

When a certain ideal engine performs 2000 kJ of work, 4750 kJ of heat flows out of the engine at 275°C. (a) How much heat flows into the engine? (b) What is the efficiency of the engine? (c) At what temperature does heat flow into the engine?

Answer 1

a) Qh= 6750 kJ

b) e = 0.296

c)
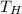`T_H` = 390.625° C

Step-by-step explanation:

Given:

Work done, W = 2000 kJ

Heat flow, Q = 4750 kJ

Temperature at which heat flows out,
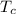`T_c` = 275° C

a) Now, the heat flow through the engine (Qh)

Qh = W + Q

or

Qh = 2000 + 4750

or

Qh= 6750 kJ

b) The efficiency (e) is given as:

`e=(W)/(Q_h)`

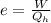
on substituting the values, we get

`e=(2000)/(6750)`

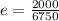
or

e = 0.296

c)
`e=1-(T_c)/(T_H)`

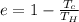
where,

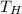`T_H` is the temperature at which heat flow

on substituting the values, we get

`0.296=1-(275)/(T_H)`

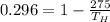
or

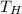`T_H` = 390.625° C