Question

A pot of water is boiling under one atmosphere of pressure. Assume that heat enters the pot only through its bottom, which is copper and rests on a heating element. In two minutes, the mass of water boiled away is m = 4.5 kg. The radius of the pot bottom is R = 6.5 cm and the thickness is L = 2.0 mm. What is the temperature of the heating element in contact with the pot?

Answer 1

Step-by-step explanation:

It is given that,

Mass of boiled water, m = 4.5 kg

Radius of the pot bottom, r = 6.5 cm = 0.065 m

Thickness of the pot, t = 2 mm = 0.002 m

We need to find the temperature of the heating element in contact with the pot.

Heat transferred is from pot to water is given by :

`H=(kA(T_2-T_1))/(l)`

`(Q)/(t)=(kA(T_2-T_1))/(l)`

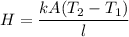
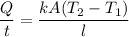
T₁ is the boiling temperature of water, T₁ = 100⁰ C

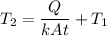`T_2=(Q)/(kAt)+T_1`, q = m L, L is the latent heat of vaporization

`T_2=(mL)/(kAt)+T_1`,

k is the thermal conductivity of water,
`k=390\ Jm^(-1)s^(-1)(^oC)^(-1)`

`L=2.26* 10^6\  Jkg^(-1)`

`T_2=(4.5* 2.26* 10^6)/(390* \pi* (0.065)^2* 120)+100`

`T_2=1737.18\ ^oC`

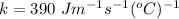
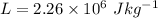
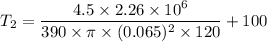
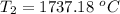
Hence, this is the required solution.