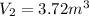Answer:
The correct answer is option c.
Step-by-step explanation:
Using An deal gas equation:
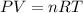
V = Volume of the gas at given pressure P and Temperature T.
n= number of moles
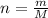
m = Mass of the gas
M= Molar mass of the gas
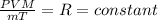
Volume of the gas at 25 kPa and 120°C,
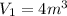
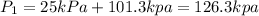
(Absolute pressure is equal to sum of gauge pressure ant atmospheric pressure.)
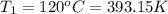
Moles of gas ,
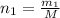
 ...(1)
...(1)
Volume of the gas at 101.3 kPa and 20°C,
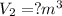
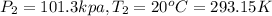
Moles of gas ,
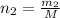
Volume asked for the same mass of gas:
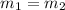
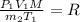 ..(2)
..(2)
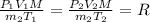
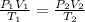
Substituting all the given values we get value of
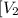 :
: