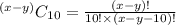Question

Sammy has x flavors of candies with which to make goody bags for Frank's birthday party. Sammy tosses out y flavors, because he doesn't like them. How many different 10–flavor bags can Sammy make from the remaining flavors? (It doesn't matter how many candies are in a bag, only how many flavors.)

Answer 1

`^((x-y))C_(10)=((x-y)!)/(10! * (x-y-10)!)`

Explanation:

Total flavors Sammy initially had = x

Number of flavors Sammy throw away = y

After throwing away y flavors, the number of flavors Sammy will be left with = x - y

He needs to make 10-flavor bags from these (x - y) flavors. In order words he needs to chose 10 flavors for each bag from(x - y) flavors. The order of selection is not important here, so this is a problem of combinations. Also since we have to make selections or small groups, this also indicates that we have to use combinations.

So we need to make combinations of 10 flavors from a total of (x - y) flavors. This can be represented as
`^((x-y))C_(10)`

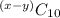
The formula for combinations is:

`^(n)C_(r)=(n!)/(r!(n-r)!)`

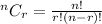
Using the values in this formula, we get:

`^((x-y))C_(10)=((x-y)!)/(10! * (x-y-10)!)`