Question

Y=7x+3 7x-6y=-18 substitution

Answer 1

`y=3`

`x=0`

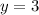
Explanation:

we have the following system of equations:

`y=7x+3\\7x-6y=-18`

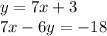
the substitution method requires that we take one of the variables of one equation, and substitute that value in the other equation.

in this case taking advantage of the fact that in the first equation the value of
`y` is already cleared, we substitute it in the second equation:

`7x-6(7x+3)=-18`

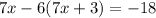
and then we solve for x:

`7x-42x-18=-18\\-35x-18=-18\\-35x=-18+18\\-35x=0\\x=0`

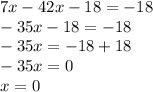
and since x=0 substituting this into the first equation of the system to find the value of
`y`:

`y=7(0)+3\\y=3`

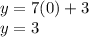
the answer is
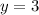`y=3` and
`x=0`

Answer 2

x=0

y=3

Explanation:

y =7x+3 equation 1

7x-6y=-18 equation 2

using equation 1 in equation 2 we have:

7x-6(7x+3)= -18

7x -42x -18 = -18

-35x -18 = -18

-35x = -18 +18

-35x=0

x=0

so we have:

y =7x+3

y= 7(0) +3

y = 3