Question

Which of the following points are more than 5 units from the point P(-2, -2)?

Select all that apply.
A. A(1, 2)
B. B(3, −1)
C. C(2, −3)
D. D(−6, −6)
E. E(−4, 1)

Answer 1

Answer:D

Explanation:

Answer 2

B(3,-1),D.(-6,-6)

Explanation:

Hello

the distance between two points is equal to the length of the line segment that joins them, expressed numerically.

Let 2 points

`A(x_(1),y_(1)) \\B(x_(2),y_(2)) \\\\D=\sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)  }`

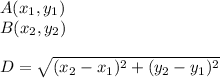
all you have to do is to find the distance between P and each point replacing the values.

Step 1

P(-2,-2)

A(1,2)

hence

`D=\sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)  } \\D=\sqrt{(1-(-2))^(2)+(2-(-2)^(2)  }\\D=\sqrt{(3)^(2)+(4)^(2)  }\\\\D=√(9+16) \\D=√(25) \\D=5`

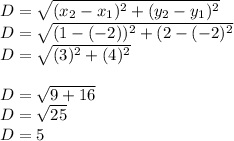
so, A is not more than 5 units from P

Step 2

P(-2,-2)

B(3,-1)

hence

`D=\sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)  } \\D=\sqrt{(3-(-2))^(2)+(-1-(-2)^(2)  }\\D=\sqrt{(5)^(2)+(1)^(2)  }\\\\D=√(25+1) \\D=√(26) \\D=5.099`

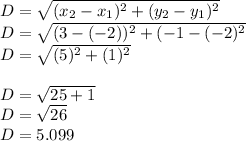
so, B is more than 5 units from P

Step 3

P(-2,-2)

C(2,-3)

hence

`D=\sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)  } \\D=\sqrt{(2-(-2))^(2)+(-3-(-2)^(2)  }\\D=\sqrt{(4)^(2)+(-1)^(2)  }\\\\D=√(16+1) \\D=√(17) \\D=4.123`

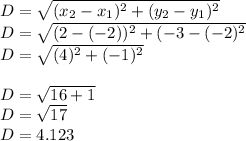
so, C is not more than 5 units from P

Step 4

P(-2,-2)

D(-6,-6)

hence

`D=\sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)  } \\D=\sqrt{(-6-(-2))^(2)+(-6-(-2)^(2)  }\\D=\sqrt{(-4)^(2)+(-4)^(2)  }\\\\D=√(16+16) \\D=√(32) \\D=5.65`

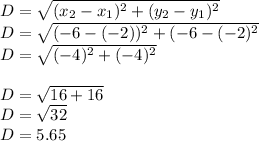
so, D is more than 5 units from P

Step 5

P(-2,-2)

E(-4,1)

hence

`D=\sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)  } \\D=\sqrt{(-4-(-2))^(2)+(1-(-2)^(2)  }\\D=\sqrt{(-2)^(2)+(3)^(2)  }\\\\D=√(4+9) \\D=√(13) \\D=3.60`

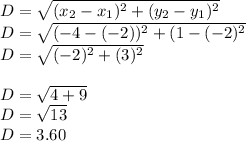
so, E is not more than 5 units from P

Have a great day.