Question

A box of mass m = 4 kg is suspended vertically from a spring with stiffness k = 64 N/m. Determine the position of the box as a function of time if at t = 0, x = 0 and = 2 m/s.

Answer 1

x=0.5 sin 4 t

Step-by-step explanation:

Given that:

mass m = 4 kg

Stiffness K =64 N/m

Given spring mass system will be in simple harmonic motion.We know that in simple harmonic motion the natural frequency given as follows

`\omega _n=\sqrt{(K)/(m)}`

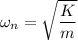
Now by putting the values

`\omega _n=\sqrt{(64)/(4)}`

`\omega _n=4 rad/s`

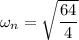
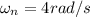
The equation of SHM given as

`\ddot{x}+\omega _n^2x=0`

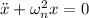
The solution of above equation will be

`x=Asin\omega _nt`

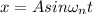
x=A sin 4 t

Given at t=0 ,V= 2 m/s

So

V= 4 A cos 4 t

2 = 4 A

A= 0.5

The equation of motion will be

x=0.5 sin 4 t