Step-by-step explanation:
Capacitance,
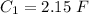
Capacitance,
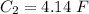
Capacitance,
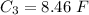
Capacitors C₁ and C₂ are connected in series. The equivalent capacitance is given by :
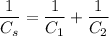
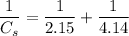
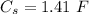
The combination is now connected with C₃ in parallel. Now the equivalent capacitance is given by :
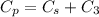
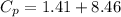
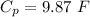
So, the equivalent capacitance of the total combination is 9.87 F. Hence, this is the required solution.