Answer:
-5
negative nine-halves
Explanation:
we know that
In the quadratic equation

If
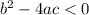
then
The system has no real numbers solutions
we have
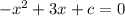
so

substitute
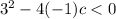
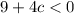
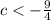
Verify each case
case 1) -5
For c=-5
substitute
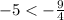
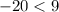 ------> is true
------> is true
therefore
The value of c=-5 will cause the quadratic equation to have no real number solutions
case 2) negative nine-halves
For c=-9/2
substitute
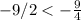
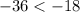 ------> is true
------> is true
therefore
The value of c=-9/2 will cause the quadratic equation to have no real number solutions
case 3) negative one-quarter
For c=-1/4
substitute
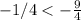
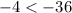 ------> is not true
------> is not true
therefore
The value of c=-1/4 will not cause the quadratic equation to have no real number solutions
case 4) 1
For c=1
substitute
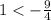 ------> is not true
------> is not true
therefore
The value of c=1 will not cause the quadratic equation to have no real number solutions
case 5) 9 Over 4
For c=9/4
substitute
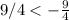 ------> is not true
------> is not true
therefore
The value of c=9/4 will not cause the quadratic equation to have no real number solutions