Answer:

Explanation:
We know that the volume of one of the cylinders is:

And the volume of the other cylinder is:
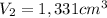
Then, by definition, the scale factor is:
![scale\ factor=\sqrt[3]{(V_1)/(V_2) }](https://img.qammunity.org/2020/formulas/mathematics/high-school/iywkkjlrya63hgqjfgmfi78brj0hjejwjr.png)
Therefore, substitute the volumes into the expression, we get that the scale factor betweeen these cylinders is:
![scale\ factor=\sqrt[3]{(27 cm^3)/(1,331 cm^3.) }\\\\scale\ factor=(3)/(11)](https://img.qammunity.org/2020/formulas/mathematics/high-school/vfhgcck7wc4a1w5p6ugzpllfwish8uv0st.png)