Question

A compact disk manufacturer charges $100 for each box of CDs ordered. However, it reduces the price by S1 per box for each box in excess of 50 boxes but less than 100 boxes. Determine the number of boxes of CDs that should be sold to maximize revenue. What is the maximum revenue? To maximize revenue, boxes of CDs should be sold

Answer 1

75 CD's should be sold and maximum revenue is $ 2500.

Explanation:

Given,

The original charges for each CD = $ 100,

∵ it reduces the price by $ 1 per box for each box in excess of 50 boxes but less than 100 boxes.

That is, the charges would be (100-x) dollars for (50 + x) CD's

Where, 50 + x ≤ 100 and x ≥ 0,

Thus, the total revenue = number of CD's × price of each Cd

R(x) = (50+x)(100-x)

`\implies R(x) = 5000-50x + 100x -x^2`

`=5000+50x-x^2`

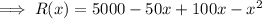
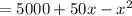
Differentiating with respect to x,

`R'(x) = 50 - 2x`

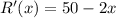
Again differentiating with respect to x,

`R''(x) = -2`

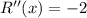
For maxima or minima,

R'(x) = 0

`50-2x=0\implies x=25`

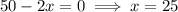
For x = 25, R''(x) = negative,

Hence, the revenue is maximum for the additional CD's 25,

Maximum revenue, R(25) = 5000 + 50(25) - 625 = $ 2500

Thus, the total number of CD's that should be sold to maximise the revenue = 50 + 25 = 75.