Answer:
75 CD's should be sold and maximum revenue is $ 2500.
Explanation:
Given,
The original charges for each CD = $ 100,
∵ it reduces the price by $ 1 per box for each box in excess of 50 boxes but less than 100 boxes.
That is, the charges would be (100-x) dollars for (50 + x) CD's
Where, 50 + x ≤ 100 and x ≥ 0,
Thus, the total revenue = number of CD's × price of each Cd
R(x) = (50+x)(100-x)
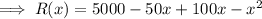
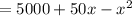
Differentiating with respect to x,
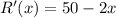
Again differentiating with respect to x,
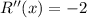
For maxima or minima,
R'(x) = 0
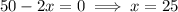
For x = 25, R''(x) = negative,
Hence, the revenue is maximum for the additional CD's 25,
Maximum revenue, R(25) = 5000 + 50(25) - 625 = $ 2500
Thus, the total number of CD's that should be sold to maximise the revenue = 50 + 25 = 75.