Question

A 7-cm diameter horizontal pipe connected to the side of a tank at 4 m below the water surface in the tank discharges water to the atmosphere. A pump located in the pipe can add head to the flow by the relation, hp (m) = 8 - 200 Q^2 (Q in m^3/s) If the losses in the system amounts to 5 m, determine the outflow velocity of the pipe.

Answer 1

47.10 m/s

Step-by-step explanation:

Diameter of the horizontal pipe, d = 7 cm = 0.07 m

Area of the horizontal pipe, A =
`(\pi)/(4)d^2`

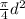
or

A =
`(\pi)/(4)0.07^2` = 0.00384 m²

Head between the water surface and the pipe level, z = 4 m

Head added by the pump, hp = 8 - 200Q²

where, Q is the discharge

losses, hL = 5 m

now,

applying the Bernoulli's theorem between the water surface and the pipe outlet,

we have

`(P_1)/(\rho)+(V_1^2)/(2g)+z+h_P=(P_2)/(\rho)+(V_2^2)/(2g)+h_L`

where,

P₁ = pressure at the water surface = 0 (as atmospheric pressure only)

V₁ = Velocity at the free surface = 0

ρ is the density of the water

P₂ = pressure at the outlet = 0 (as atmospheric pressure only)

V₂ = Velocity at the outlet

on substituting the values, we get

`z+h_P=(V_2^2)/(2g)+h_L`

or

`4+(8-200Q^2)=(V_2^2)/(2*9.81)+5`

or

`7-200Q^2=(V_2^2)/(2*9.81)`

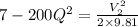
also,

Q = A × V₂

thus,

`7-200*(0.00384*\ V_2)^2=(V_2^2)/(2*9.81)`

or

V₂ = 47.10 m/s