Question

Can someone answer #4 and 5 please

Answer 1

4)

If you know the slope
`m` and a point
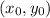`(x_0,y_0)` belonging to a line, then the equation of the line is

`y-y_0=m(x-x_0)`

In your case, you have
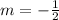`m=-(1)/(2)` and
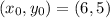`(x_0,y_0)=(6,5)`. So, the equation of the line is

`y-5=-(1)/(2)(x-6) \iff y = -(1)/(2)x+8`

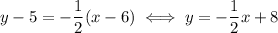
5)

If you know two points
`(x_1,y_1),\ (x_2,y_2)` belonging to a line, then the equation of the line is

`(y-y_2)/(y_1-y_2)=(x-x_2)/(x_1-x_2)`

In your case, you have
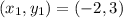`(x_1,y_1)=(-2,3)` and
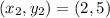`(x_2,y_2)=(2,5)`. So, the equation of the line is

`(y-5)/(3-5)=(x-2)/(-2-2) \iff (y-5)/(-8)=(x-2)/(-4) \iff y-5 = 2x-4 \iff y = 2x+1`

Answer 2

Answer:
`\bold{4)\quad y=-(1)/(2)x+8}`

`\bold{5)\quad y=(1)/(2)x+4}`

Explanation:

Use the Point-Slope formula: y - y₁ = m(x - x₁) where

• (x₁ , y₁) is a point
• m is the slope

`y-5=-(1)/(2)(x-6)\\\\\\y-5=-(1)/(2)x+3\\\\\\.\quad \large\boxed{y=-(1)/(2)x+8}`

*****************************************************************************

Find the slope using the formula:
`m=(y_2-y_1)/(x_2-x_1)`

Then use the Point-Slope formula using ONE of the points as (x₁ , y₁)

`m=(5-3)/(2-(-2))=(2)/(4)=\boxed{(1)/(2)}`

`y-5=(1)/(2)(x-2)\\\\\\y-5=(1)/(2)x-1\\\\\\.\quad \large\boxed{y=(1)/(2)x+4}`