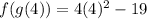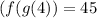Question

For f(x)=4x+1 and g(x)=x^2-5,find(f•g)(4)

Answer 1

45

Explanation:

Assuming f∘g, it is the function composition of two given function. So, f(g(x))=(f∘g)(x).

Function Composition is when we nest two functions creating another one, so if we nest f(x) and g(x) we'll have another one f(g(x)).

If f(x)=4x+1 and g(x)=x^2-5, (fg)(x)

If we replace x in the second function, namely, g(x) then we have:

f(g(x))

`4(x^2-5)+1=0\\\\4x^2-20+1=0\\\\4x^2-19=0`

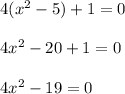
Now, let's plug it in the value of 4 for x

`f(g(4))=4(4)^2-19\\`

`(f(g(4))=45`

Answer 2

(f•g)(4) = 45

Explanation:

f(x)=4x+1

g(x)=x^2-5

(f•g)(x) = 4(x^2 -5)+1

(f•g)(4) = 4(4^2 -5)+1

(f•g)(4) = 4(16-5)+1

(f•g)(4) = 4(11)+1

(f•g)(4) = 44 + 1

(f•g)(4) = 45