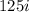Answer:
Explanation:
When we have potential expression that include imaginary numbers, we have to consider some basic results, because these imaginary potential expression are cyclical.
We know that:
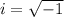
So, elevating both members to a third power, we have:
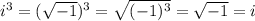
So,
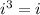 , which is the beginning, that's why we say that it's like a cycle.
, which is the beginning, that's why we say that it's like a cycle.
So, from the problem, we have:
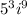
To solve this, we consider the operations from the beginning:
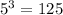 ; and
; and
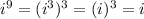 ; because
; because
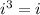
Therefore, the result would be