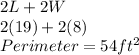Question

A rectangle has a length that is 3 more than twice its width. If its area is 152ft^2, what is its perimeter

Answer 1

`Perimeter=54ft^2`

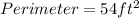
Explanation:

Let's start by writing what we know in mathematical terms.

A rectangle has a length that is 3 more than twice its width, means:

`L-3 = 2W\\L*W = 152`

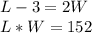
Now all we have to do is solve for one of these values. I'll choose W.

Rewrite the equation:

`L = 2W + 3`

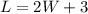
Input that information into our second equation and solve:

`W*(2W + 3) = 152\\2W^2+3W=152\\2W^2+3W-152=0`

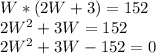
Find the two W values by factoring the equation (note that the Width can't be negative because you can't have a negative rectangle):

`2W^2+3W-152=0\\(2W+19)(W-8)=0\\\\W=-(19)/(2)\\W=8`

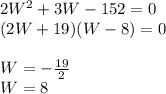
We pick the positive value 8 and plug it into our original equation to find Length:

`L = 2W + 3\\L=2(8)+3\\L=19`

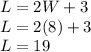
Finally, after all that, we can use the formula of a perimeter using our newly found Length and Width values (remember not to forget "ft^2" when we get our answer):

`2L+2W\\2(19)+2(8)\\Perimeter=54ft^2`