Answer:
![\left[\begin{array}{ccc}0&1&0\\1&0&0\\0&0&0\end{array}\right],\left[\begin{array}{ccc}0&1&0\\1&0&0\\0&0&0\end{array}\right],\left[\begin{array}{ccc}0&1&0\\1&0&1\\0&1&0\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/b2dxj0p10i6yspcbo0633g1o2xths8ofwq.png)
Explanation:
We are given that vector space of all symmetric matrix
M(R)={
![\left[\begin{array}{ccc}a&b&c\\d&e&f\\g&h&i\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/xbtktg5en9ny4jcfwnwtgcityfkq1t3t08.png)
where a,b,c,d,e,f,g,h,i
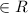 }
}
Let A=
![\left[\begin{array}{ccc}a&b&c\\d&e&f\\g&h&i\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/xbtktg5en9ny4jcfwnwtgcityfkq1t3t08.png)
A'=
![\left[\begin{array}{ccc}a&d&g\\b&e&h\\c&f&i\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/uqf2mbwyclswtumuelokqc2k0dhbj8b280.png)
A is symmetric
Then A'=A
![\left[\begin{array}{ccc}a&b&c\\d&e&f\\g&h&i\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/xbtktg5en9ny4jcfwnwtgcityfkq1t3t08.png) =
=
![\left[\begin{array}{ccc}a&d&g\\b&e&h\\c&f&i\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/uqf2mbwyclswtumuelokqc2k0dhbj8b280.png)
a=a , e=e, i=i
a-a=0 , e-e=0, i-i=0
b=d, c=g ,f=h
Hence, the matrix
![\left[\begin{array}{ccc}0&b&c\\b&0&f\\c&f&0\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/azou6n0e5ej3gtm4f2iemz3mfxx8kg5wtv.png)
Therefore, the basis are
![\left[\begin{array}{ccc}0&1&0\\1&0&0\\0&0&0\end{array}\right],\left[\begin{array}{ccc}0&1&0\\1&0&0\\0&0&0\end{array}\right],\left[\begin{array}{ccc}0&1&0\\1&0&1\\0&1&0\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/b2dxj0p10i6yspcbo0633g1o2xths8ofwq.png)
There are three elements to generate an element of vectors of all symmetric matrix
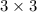 matrix
matrix
![\left[\begin{array}{ccc}0&b&c\\b&0&f\\c&f&0\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/azou6n0e5ej3gtm4f2iemz3mfxx8kg5wtv.png) =
=
![b\left[\begin{array}{ccc}0&1&0\\1&0&0\\0&0&0\end{array}\right]+c\left[\begin{array}{ccc}0&1&0\\1&0&0\\0&0&0\end{array}\right]+f\left[\begin{array}{ccc}0&1&0\\1&0&1\\0&1&0\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/2vl6y4aj1lbtwcwzr2yiplf7tnng4ow31c.png)