Question

A thin plate of steel contains a crack of length 2a =16 mm, which is subjected to a stress of 350 MPa. The yield stress of the material is 1000 MPa. The radius of the plastic region is approximately

Answer 1

0.49 mm

Step-by-step explanation:

Given:

Crack length, 2a = 16 mm

or

a = 8 mm = 0.008 m

Applied stress, σ = 350 MPa

Yield stress,
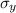`\sigma_y` = 1000 MPa

Now,

The stress intensity factor (K) is given as:

K = σ√(πa)

on substituting the values, we get

K = 350 × √(π × 0.008)

or

K = 55.48

also,

from Irwin's plastic zone correction factor

we have the formula

`r_p=(1)/(2\pi)((K)/(\sigma_y))^2`

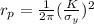
where,

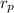`r_p` is the radius of the plastic zone

on substituting the respective values, we get

`r_p=(1)/(2\pi)((55.48)/(1000))^2`

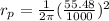
or

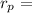`r_p=` 0.00049 m

or

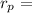`r_p=`0.49 mm