Question

Suppose you start with a sample with 6.030×10^8 nuclei of a particular isotope. This isotope has a half-life of 537 s. What is the decay constant for this particular isotope? How many nuclei remain after 1.50×10^3 s?

What is the activity of the sample at the beginning of the experiment?

Answer 1

decay constant is 1.290 ×
`10^(-3)` s-1

Number is 0.870 ×
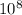`10^(8)` nuclei

activity is 1.1223 ×
`10^(5)` Ci

Step-by-step explanation:

Given data

isotope N1 = 6.030×10^8 nuclei

half life T/2 = 537 s

to find out

decay constant and How many nuclei remain and activity of the sample at the beginning

solution

we know that half life and decay constant relationship that is

N = N1 ×
`e^(-kt)` ...............1

here k is decay constant and we know dN / dt is equal to -k × N

and T/2 = 0.693/k

so k = 0.693 / (T/12)

put here T/2

k = 0.693 / 537 = 1.290 ×
`10^(-3)` s-1

so decay constant is 1.290 ×
`10^(-3)` s-1

and

by equation 1 we get

N = N1 ×
`e^(-kt)`

N = 6.030×10^8 ×
`e^{-1.290  × [tex]10^(-3)` 1.50×10^3}[/tex]

N = 0.870 ×
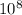`10^(8)` nuclei

and

we know Activity of sample =k×N

so

activity = 0.870 ×
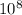`10^(8)` × 1.290 ×
`10^(-3)`

activity = 1.1223 ×
`10^(5)` Ci