Step-by-step explanation:
Given that,
Time = 3.8 days
Radon exposure = 400 Bq/m³
Dangerous level = 8000 Bq/m³
Time = 16 days
We need to calculate the decay constant
Using formula of decay constant
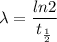
Put the value into the formula
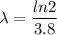
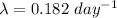
Now,
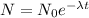
Put the value into the formula

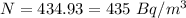
It is still not safe to enter the house after 16 days.
(B). We need to calculate the Richter Scale measurement for an earthquake
Given that,
Earthquake measurement = 8.2
 ....(I)
....(I)
Using formula for Richter Scale measurement
We know that,
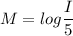
For Earthquake of magnitude,
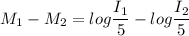
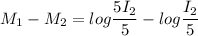
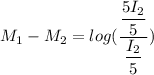
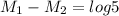
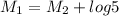
Put the value into the formula
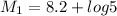

Earthquake of magnitude 8.9 will be about 5 times as strong as earthquake of magnitude 8.2.
Hence, This is the required solution.