Answer with Step-by-step explanation:
Suppose a positive integer n.
We have to prove that if n is even , then 7n+4 is even .
We are given some steps in order to prove this we have to arrange in correct order.
If n is even, it can be written as 2k
n=2k for some integer k
Then substitute the value of n then we get
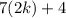

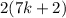
This is 2 times an integer , so it is even.
Hence, proved.