Question

A circular coil of wire having a diameter of 20.0 cm and 3000 turns is placed in the earth's magnetic field with the normal of the coil parallel to the field vector. At what angular frequency must the loop be rotated to produce a 1.5 V emf amplitude? Assume that the magnitude of the earth's field is 1.0 x 10^-4 T.

Answer 1

Explanation :

It is given that,

Diameter of the coil, d = 20 cm = 0.2 m

Radius of the coil, r = 0.1 m

Number of turns, N = 3000

Induced EMF,
`\epsilon=1.5\ V`

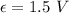
Magnitude of Earth's field,
`B=10^(-4)\ T`

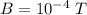
We need to find the angular frequency with which it is rotated. The induced emf due to rotation is given by :

`\epsilon=NBA\omega`

`\omega=(\epsilon)/(NBA)`

`\omega=(1.5)/(3000* 10^(-4)* \pi (0.1)^2)`

`\omega=159.15\ rad/s`

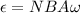
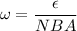
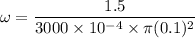
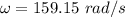
So, the angular frequency with which the loop is rotated is 159.15 rad/s. Hence, this is the required solution.