Question

The power of a lens is defined as the reciprocal of its focal length: P = 1/f. (Thus power is measured in inverse meters, called diopters.) Given two thin lenses of specified power and their separation, calculate the power of the combination. Remember that the image produced by the first lens becomes an object for the second.

Answer 1

This the power of combination is given by

`P_(combination)=(1)/(F)=(d+f_(2)-f_(1))/(f_(2)(d-f_(1)))`

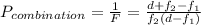
Step-by-step explanation:

Let 'F' be the focal length of the combination of the two lenses and the focal length's of individual lenses be
`f_(1),f_(2)`

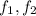
We know that focal length is the position of image when object is placed at infinity

Let us place the the object at infinity with respect to the first lens thus the position of image formed by the first lens shall be obtained using lens formula as

`(1)/(f_(1))=(1)/(u)+(1)/(v)`

Applying values we get

`(1)/(f_(1))=(1)/(\infty )+(1)/(v)\\\\\Rightarrow (1)/(f)=0+(1)/(v)\\\\\therefore v=+f_(1)`

Now this position of image formed by the first lens act's as object for the second lens, thus we have

`(1)/(f_(2))=(1)/(-(d-f_(1)))+(1)/(v)\\\\\Rightarrow (1)/(f_(2))+(1)/(d-f_(1))=(1)/(v)\\\\\therefore (1)/(v)=((d-f_(1))+f_(2))/(f_(2)(d-f_(1)))\\\\=(1)/(v)=(d+f_(2)-f_(1))/(f_(2)(d-f_(1)))\\\\\therefore v_(f)=(f_(2)(d-f_(1)))/(d+f_(2)-f_(1))`

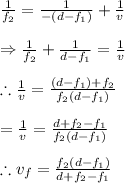
Since image of an object placed at infinity will be formed at
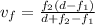`v_(f)=(f_(2)(d-f_(1)))/(d+f_(2)-f_(1))` thus the focal length of the combination of the 2 thin lenses will be
`F=(f_(2)(d-f_(1)))/(d+f_(2)-f_(1))`

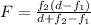
This the power of combination is given by

`P_(combination)=(1)/(F)=(d+f_(2)-f_(1))/(f_(2)(d-f_(1)))`

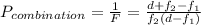
(For the sake of question we assume lenses to be convex although the same procedure is valid for all other lenses)