Question

If the coordinate of RST are R(0,0), S(7,0), and T(2,5), what is the sum of the slopes of the three sides of the triangle.

Answer 1

The sum of the slopes of the three sides of the triangle is 3/2.

Explanation:

Given information: The vertices of triangle are R(0,0), S(7,0), and T(2,5).

We need to find the sum of the slopes of the three sides of the triangle.

Slope formula:

`m=(y_2-y_1)/(x_2-x_1)`

Using slope formula, the slope of segment RS is

`m_(RS)=(0-0)/(7-0)=0`

`m_(RT)=(5-0)/(2-0)=(5)/(2)`

`m_(ST)=(5-0)/(2-7)=(5)/(-5)=-1`

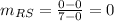
The sum of the slopes of the three sides of the triangle is

`Sum=m_(RS)+m_(RT)+m_(ST)`

`Sum=0+(5)/(2)+(-1)`

`Sum=(5-2)/(2)`

`Sum=(3)/(2)`

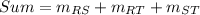
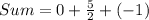
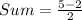
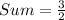
Therefore the sum of the slopes of the three sides of the triangle is 3/2.