Question

Use the Divergence Test to determine whether the following series diverges or state that the test is inconclusive. Summation from k equals 0 to infinity StartFraction 1 Over 1000 plus k EndFraction

Answer 1

The test is inconclusive.

Explanation:

Let us assume that the series is
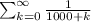`\sum_(k=0)^\infty (1)/(1000+k)`. The Divergence Test tell us that, if the limit of the sequence defined by the general term of the series:
`\lim_(k\rightarrow \infty)a_k`, is different from zero, or it doesn't exist, then the series diverges.

In this exercise we have
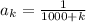`a_k= (1)/(1000+k)`, then the limit we want to study is

`\lim_(k\rightarrow \infty) (1)/(1000+k).`

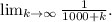
It is not difficult to see that if
`k` grows to infinity,the limit of the given fraction is zero:

`\lim_(k\rightarrow \infty) (1)/(1000+k)=0.`

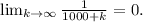
Thus, the convergence test is inconclusive. Recall the case of the harmonic series:
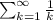`\sum_(k=1)^\infty (1)/(k)`, which is divergent and clearly
`\lim_(k\rightarrow \infty)(1)/(k)=0`.