Question

According to Kepler's Third Law, a solar-system planet that has an orbital period of 8 years would have an orbital radius of about ________ year(s)

Answer 1

Orbital period, T = 1.42 years

Step-by-step explanation:

It is given that,

Orbital period of a solar system planet,
`T=8\ years=2.52* 10^(8)\ s`

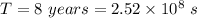
The orbital period of the planet can be calculated using third law of Kepler's. It is as follows :

`T^2=(4\pi^2)/(GM)r^3`

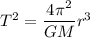
M is the mass of the sun

`r^3=(T^2GM)/(4\pi^2)`

`r^3=((2.52* 10^(8))^2* 6.67* 10^(-11)* 1.989* 10^(30))/(4\pi^2)`

`r^3=2.134* 10^(35)`

`r=5.975* 10^(11)\ m`

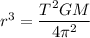
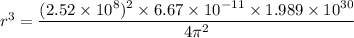
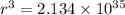
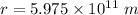
r = 1.42 AU

So, the solar-system planet that has an orbital period of 8 years would have an orbital radius of about 1.42 AU.