Question

A mass suspended on a spring will exhibit sinusoidal motion when it moves. If the mass on a spring is 85 cm off the ground at its highest position and 41 cm off the ground at its lowest position and takes 3.0 s to go from the top to the bottom and back again, determine an equation to model the data.

Answer 1

Using equation

y(t)=y0*Cos(wt)

w=2
`\pi`/3

y0=85-41

y(t)=44cos(2
`\pi`/3*t)

Answer 2

The equation of motion is
`y(t)=22sin((2\pi )/(3)t)`

Step-by-step explanation:

The general equation of motion of a SHM motion is given by

`y(t)=Asin(\omega t+\phi )`

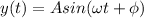
where,

A is the amplitude of the motion

ω is the natural frequency of the system

Since amplitude is defines as the maximum displacement of the object from the mean position we have

`2A=85 cm-41 cm\\\\A=(44)/(2)cm\\\\\therefore A=22cm`

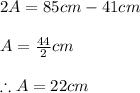
Now the time period is related to the natural angular frequency as

`\omega =(2\pi )/(T)\\\\\therefore \omega=(2\pi )/(3)`

Thus the equation of motion becomes

`y(t)=22sin((2\pi )/(3)t+\phi )`

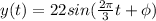
the initial phase can be assumed to be zero thus the equation becomes

`y(t)=22sin((2\pi )/(3)t)`