Answer:
The intrinsic carrier density of diamond is
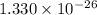 .
.
Step-by-step explanation:
Given that,
Energy band gape = 5.4 eV
Temperature = 300 K
We need to calculate the intrinsic carrier density of diamond
Using formula of density
 ....(I)
....(I)
We need to calculate
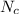
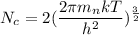
Put the value into the formula
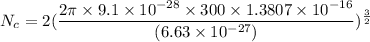

We need to calculate
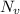
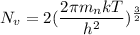
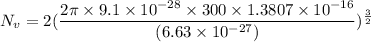

So.
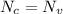
Now, Put the value of
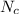 and
and
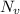 in equation (I)
in equation (I)
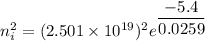
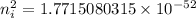
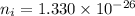
Hence, The intrinsic carrier density of diamond is
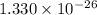 .
.