Question

A person hears a siren as a fire truck approaches and passes by. The frequency varies from 480Hz on approach to 400Hz going away. What is the speed of the truck if the speed of sound in air is 343m/s?

Answer 1

31.2 m/s

Step-by-step explanation:

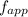`f_(app)` = Frequency of approach = 480 Hz

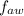`f_(aw)` = Frequency of going away = 400 Hz

`V` = Speed of sound in air = 343 m/s

`v` = Speed of truck

Frequency of approach is given as

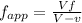`f_(app) = (Vf)/(V - v)` eq-1

Frequency of moving awayy is given as

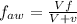`f_(aw) = (Vf)/(V + v)` eq-2

Dividing eq-1 by eq-2

`(f_(app))/(f_(aw)) = (V + v)/(V - v)`

`(480)/(400) = (343 + v)/(343 - v)`

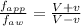
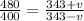
`v` = 31.2 m/s