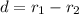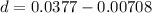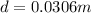Question

A charge of -3.02 μC is fixed in place. From a horizontal distance of 0.0377 m, a particle of mass 9.43 x 10^-3 kg and charge -9.78 μC is fired with an initial speed of 80.4 m/s directly toward the fixed charge. How far does the particle travel before its speed is zero?

Answer 1

`d = 0.0306 m`

Step-by-step explanation:

Here we know that for the given system of charge we have no loss of energy as there is no friction force on it

So we will have

`U + K = constant`

`(kq_1q_2)/(r_1) + (1)/(2)mv_1^2 = (kq_1q_2)/(r_2) + (1)/(2)mv_2^2`

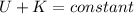
now we know when particle will reach the closest distance then due to electrostatic repulsion the speed will become zero.

So we have

`((9 * 10^9)(3.02 \mu C)(9.78 \mu C))/(0.0377) + (1)/(2)(9.43 * 10^(-3))(80.4)^2 = ((9 * 10^9)(3.02 \mu C)(9.78 \mu C))/(r) + 0`

`7.05 + 30.5 = (0.266)/(r)`

`r = 7.08 * 10^(-3) m`

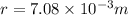
so distance moved by the particle is given as

`d = r_1 - r_2`

`d = 0.0377 - 0.00708`

`d = 0.0306 m`