Answer:
0.253 m
Step-by-step explanation:
Given that, the mass of the particle,
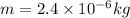 .
.
Charge of the particle,
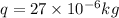 .
.
Speed of the particle,
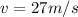 .
.
Magnetic field is,
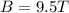 .
.
The radius of the particle's circular path when the speed of the particle is perpendicular to the magnetic field is,
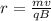 .
.
By putting all the values in the above equation.
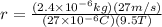 .
.
Therefore by further solving,

Therefore the radius of the particle in a circular path is 0.253 m