Answer:
The eigenvectors of the matrix are
 ,
,
 and
and
 .
.
Explanation:
The given matrix is
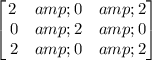
It is given that the matrix has eigenvalues 0, 2, and 4.
For
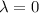
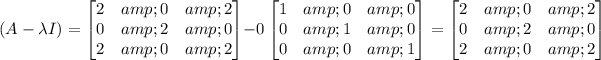

Using Row operations we get
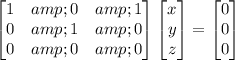
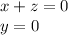
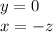
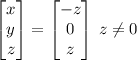
Let z=1,

At
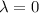 eigen vector is
eigen vector is
 .
.
Similarly,
For
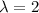
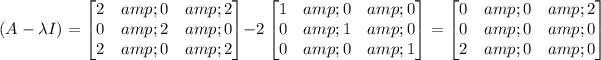
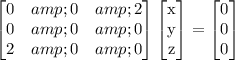
Using row operations.
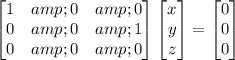
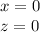
At
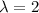 eigen vector is
eigen vector is
 .
.
For
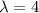

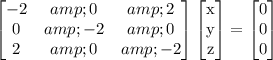
Using row operations.
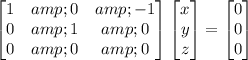
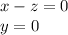
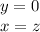
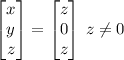
at z=1

At
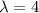 eigen vector is
eigen vector is
 .
.
Therefore the eigenvectors of the matrix are
 ,
,
 and
and
 .
.