Question

An aluminium alloy bar of diameter 12.5 mm and length 27 m loaded in uniaxial tension to a force of 3 kN. Determine the length of the bar when the force is applied. The elastic modulus of the aluminium alloy is 69 GPa.

Answer 1

27009.56 mm

Step-by-step explanation:

Given:

Diameter of the aluminium alloy bar, d = 12.5 mm

Length of the bar, L = 27 m = 27 × 10³ mm

Tensile force, P = 3 KN = 3 × 10³ N

Elastic modulus of the bar, E = 69 GPa = 69 × 10³ N/mm²

Now,

for the uniaxial loading, the elongation or the change in length (δ) due to the applied load is given as:

`\delta=(PL)/(AE)`

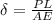
where, A is the area of the cross-section

`A=(\pi d^2)/(4)`

or

`A=(\pi*12.5^2)/(4)`

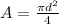
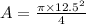
or

A = 122.718 mm²

on substituting the respective values in the formula, we get

`\delta=(3*10^3*27*10^3)/(122.718*69*10^3)`

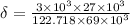
or

δ = 9.56 mm

Hence, the length after the force is applied = L + δ = 27000 + 9.56

= 27009.56 mm