Answer:
Proof
Explanation:
(a)
- We first have to show that
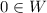 . Since
. Since
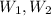 are subspaces, it holds that
are subspaces, it holds that
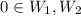 , hence
, hence
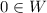 .
.
- Second, we have to show that
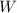 is closed under sum and scalar multiplcation. First, let us take
is closed under sum and scalar multiplcation. First, let us take
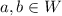 .
.
Since a, b belong to
 , we can find
, we can find
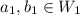 and
and
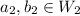 such that
such that
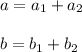
Therefore,
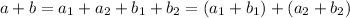
since
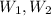 are vector subspaces of
are vector subspaces of
 , it holds that
, it holds that
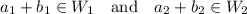 , which shows us that W is closed under sum.
, which shows us that W is closed under sum.
On the other hand, let us take
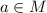 and
and
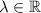 . We already know that
. We already know that
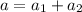
where
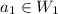 and
and
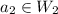 . Moreover,
. Moreover,
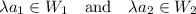 ,
,
hence

belongs to
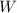 , which shows that
, which shows that
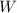 is closed under scalar multiplication.
is closed under scalar multiplication.
(b) It is clear that
 . Moreover, since
. Moreover, since
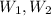 are subespaces of
are subespaces of
 , they are closed under sum and scalar multplication, this propertie is remains true for
, they are closed under sum and scalar multplication, this propertie is remains true for
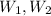 as subsets of
as subsets of
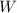 , which tells us that
, which tells us that
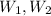 are subspaces of
are subspaces of
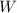 .
.