Answer with explanation:
Given : Significance level :
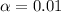
Sample size :

Degree of freedom :
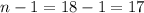
If we perform a Right- tailed test with degree of freedom 17 and significance level 0.01, then by using the chi-square distribution table , the critical value will be 33.409.
If the calculated test statistic value is greater than the critical value 33.409 then we reject the null hypothesis.