Question

What kind of problem do we need to use “indefinite integral” to solve? Use a real life example to explain.

Answer 1

Indefinite integration acts as a tool to solve many physical problems.

There are many type of problems that require an indefinite integral to solve.

Basically indefinite integration is required when we deal with quantities that vary spatially or temporally.

As an example consider the following example:

Suppose that we need to calculate the total force on a object placed in a non- uniform field.

As an example let us consider a rod of length L that posses an charge 'q' per meter length and suppose that we place it in a non uniform electric field which is given by

`E(x)=(E_(o))/(e^(kx))`

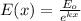
Now in order to find the total force on the rod we cannot use the similar procedure as we can see that the force on the rod varies with the position of the rod.

But if w consider an element 'dx' of the rod at a distance 'x' from the origin the force on this element will be given by

`dF=E(x)* qdx\\\\dF=(qE_(o))/(e^(kx))dx`

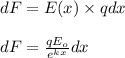
Now to find the whole force on the rod we need to sum this quantity over the whole length of the rod requiring integration, as shown

`\int dF=\int (qE_(o))/(e^(kx))dx`

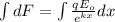
Similarly there are numerous problems considering motion of particles that require applications of indefinite integration.