Answer:
The steady deceleration,
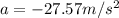
Given:
1 mile = 0.45 m/s
initial distance of the motorist, s = 50 cm
speed of the motorist at the time he noticed the traffic light, v = 90 mi/h = 90
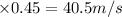
reaction time of motorist, t = 0.5 s
Solution:
Distance traveled before applying brakes, s' = v't
s' =
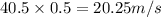
The remaining distance traveled to the traffic light, s'' = 50 - s' = 50 - 20.25 = 29.75 m
Now, using third equation of motion to calculate steady deceleration:

where
v = final velocity
u = initial velocity
s = distance traveled
a = acceleration
Now,

In this eqn w.r.t the given case v = 0, as brakes are applied and the body will decelerate as a result of braking and u = v' and s = s'' = 29.75 m
Now, eqn becomes:
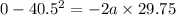
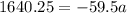
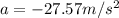
where negative sign is indicative of deceleration