Answer:
The dampening constant of the oscillation is 0.00698 kg/s.
Step-by-step explanation:
Given that,
Frequency = 1.58 Hz
Time = 46.5 s
We need to calculate the dampening constant of the oscillation
Using equation of decay of amplitude
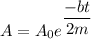 ....(I)
....(I)
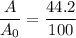
Put the value into the equation (I)
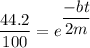
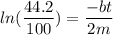
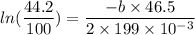
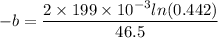
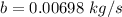
Hence, The dampening constant of the oscillation is 0.00698 kg/s.