Question

Students use a simple pendulum with a length of 36.9cm to determine the value of "g". If it takes 14.2s to complete 10 oscillations, a) what will be their experimental value "g"? b) If the pendulum were placed on the moon where "g" of the moon = 1/6th the "g" of the earth, will the period, (1) increase, (2) remain the same, (3) decrease ? and why? c) If the period on the earth were 3s, what would it be on the moon?

Answer 1

Step-by-step explanation:

It is given that,

Length of the simple pendulum, l = 36.9 cm = 0.369 m

If it takes 14.2 s to complete 10 oscillations,
`T=(14.2)/(10)=1.42\ s`

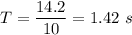
(a) The time period of the simple pendulum is given by :

`T=2\pi\sqrt{(l)/(g)}`

`g=(4\pi^2l)/(T^2)`

`g=(4\pi^2* 0.369)/((1.42)^2)`

`g=7.22\ m/s^2`

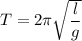
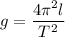
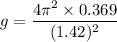
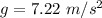
(b) On the surface of moon,
`g'=(g)/(6)`

At earth,
`g=9.8\ m/s^2`

`g'=1.63\ m/s^2`

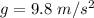
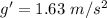
As the value of g is less on the moon, so the time period on the moon increases.

(c) The time period on the earth, T = 3 s

On earth,
`T=2\pi\sqrt{(l)/(g)}`

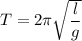
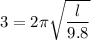`3=2\pi\sqrt{(l)/(9.8)}`..............(1)

On moon,
`T'=2\pi\sqrt{(l)/(g')}`

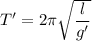
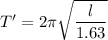`T'=2\pi\sqrt{(l)/(1.63)}`..............(2)

On solving equation (1) and (2),

T' = 18.03 s

Hence, this is the required solution.