Question

I am having trouble with problems 27, 28, 30​

Answer 1

27. d

28. b

30. c

Explanation:

27. I don't know of a way to select an appropriate answer except by computing the determinant. My preferred approach would be to let a calculator do it.

The desired determinant appears to be that of the coefficient matrix with the y-coefficients replaced by the constants on the right:

`D_y=\left|\begin{array}{ccc}2&2&-3\\4&9&6\\-2&7&9\end{array}\right|\\\\=(2)(9)(9)+(2)(6)(-2)+(-3)(4)(7)-(-2)(9)(-3)-(7)(6)(2)-(9)(4)(2)\\\\=162-24-84-54-84-72=-156 \quad\text{choice d.}`

__

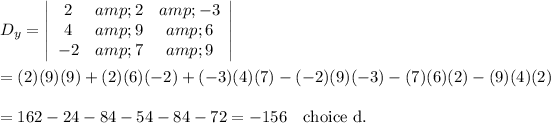
28. Same as above

`D_z=\left|\begin{array}{ccc}2&1&2\\4&-3&9\\-2&-2&7\end{array}\right|\\\\=(2)(-3)(7)+(1)(9)(-2)+(2)(4)(-2)-(-2)(-3)(2)-(-2)(9)(2)-(7)(4)(1)\\\\=-42-18-16-12+36-28=-80 \quad\text{choice b.}`

__

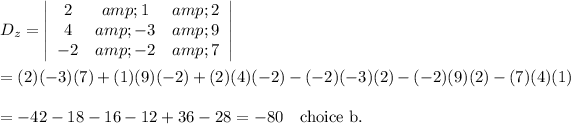
30. It works well to look at the equation for a11 and see which works:

• a. 7 - 1 ≠ 8
• b. 10 -(-9) ≠ 1
• c. 0 + 1 = 1 . . . . this works
• d. 1 - 3 ≠ 2

_____

For problems 27 and 28, we have used the "shortcut" method of finding the value of the determinant of a 3×3 matrix. That method is illustrated below. The extra two columns come from repeating the first two columns of the matrix so that it is easier to see which terms make up the "diagonals."