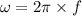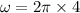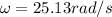Question

You observe that a mass suspended by a spring takes 0.25 s to make a full oscillation. What is the frequency of this oscillation? What is its period? What is the oscillation's angular frequency?

Answer 1

Frequency of oscillation, f = 4 Hz

time period, T = 0.25 s

Angular frequency,
`\omega = 25.13 rad/s`

Given:

Time taken to make one oscillation, T = 0.25 s

Solution:

Frequency, f of oscillation is given as the reciprocal of time taken for one oscillation and is given by:

f =
`(1)/(T)`

f =
`(1)/(0.25)`

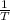
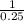
Frequency of oscillation, f = 4 Hz

The period of oscillation can be defined as the time taken by the suspended mass for completion of one oscillation.

Therefore, time period, T = 0.25 s

Angular frequency of oscillation is given by:

`\omega = 2\pi * f`

`\omega = 2\pi * 4`

`\omega = 25.13 rad/s`