Answer with explanation:
Given : The probability that telephone bills mailed to house-holds in Hong Kong are incorrect.=0.01
Binomial distribution :-
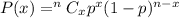
If a sample of 10 bills is selected, then the probability that at least one bill will be incorrect :-
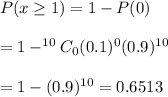
Hence, the probability that at least one bill will be incorrect =0.6513
Poisson distribution:
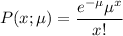
Mean :
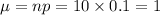
Then , If a sample of 10 bills is selected, then the probability that at least one bill will be incorrect :-
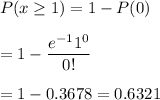
Hence, the probability that at least one bill will be incorrect =0.6321