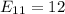Answer:
12
Explanation:
Given :
Male Female Total
Registered 60
Non registered 40
Total 20 80
Solution :
N= 100
Formula of expected frequency =
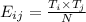
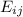 = expected frequency for the ith row/jth columm.
= expected frequency for the ith row/jth columm.
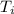 = total in the ith row
= total in the ith row
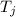 = total in the jth column
= total in the jth column
N = table grand total.
So, using formula
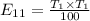
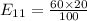
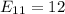
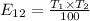
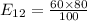
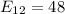
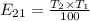
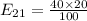
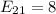
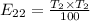
![E_{22]=(80 * 40)/(100)](https://img.qammunity.org/2020/formulas/mathematics/college/9jibxyespggw6sj4pql9tbm7xqwd3mum0h.png)
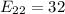
Expected frequency table
Male Female Total
Registered 12 48 60
Non registered 8 32 40
Total 20 80
So, the expected frequency for males who are registered voters are