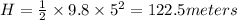Question

A man releases a stone (at rest, Vo=0) from the top of a tower. During the last second of its travel, the stone falls through a distance of (9/25)H, where H is the tower's height. Find H. Acceleration due to gravity, g=9.8 m/s². Assume no air resistance.

Answer 1

Height of tower equals 122.5 meters.

Step-by-step explanation:

Since the height of the tower is 'H' the total time of fall of stone 't' is calculated using second equation of kinematics as

Since the distance covered in last 1 second is
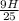`(9H)/(25)` and the total distance covered in 't' seconds is 'H' thus the distance covered in the first (t-1) seconds of the motion equals

`S_(t-1)=S_(t)-S_(last)\\\\S_(t-1)=H-(9H)/(25)=(16H)/(25)`

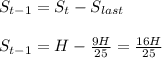
Now by second equation of kinematics we have

`S=ut+(1)/(2)gt^(2)\\\\S=(1)/(2)gt^(2)(\because u=0)`

Thus we have

`(16H)/(25)=(1)/(2)g(t-1)^(2).............(i)\\\\H=(1)/(2)gt^(2)..............(ii)`

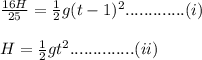
Dividing i by ii we get

`(16)/(25)=((t-1)^(2))/(t^2)\\\\\therefore (t-1)/(t)=(4)/(5)\\\\\therefore t=5secs`

Thus from equation ii we obtain 'H' as

`H=(1)/(2)* 9.8* 5^(2)=122.5meters`