Step-by-step explanation:
Orbital radius,
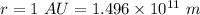
According to Kepler's law :
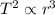
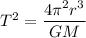
Where
M is the mass of sun,
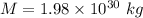
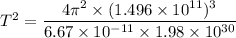
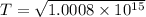
T = 31635423.18 s
or
T = 1.0003 years
So, a solar-system planet that has an orbital radius of 1 AU would have an orbital period of about 1.0003 year(s).