Question

Can someone help me work out this please A and B

Answer 1

see explanation

Explanation:

(a) (i)

x² - 9 ← is a difference of squares and factors as

(x - 3)(x + 3)

(ii)

given x² + x - 12

Consider the factors of the constant term (- 12) which sum to give the coefficient of the x- term (+ 1)

The factors are + 4 and - 3, since

4 × - 3 = - 12 and 4 - 3 = + 1, hence

x² + x - 12 = (x + 4)(x - 3)

(iii)

Express the numerator/ denominator in factored form

`(x^2-9)/(x^2+x-12)`

=
`((x-3)(x+3))/((x+4)(x-3))`

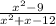
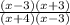
Cancel the (x - 3) factor on the numerator/denominator, leaving

=
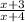`(x+3)/(x+4)` with restriction x ≠ - 4

(b)

Expand the second pair of factors using FOIL

= (x + 2)(x² + 5x - 3x - 15)

= (x + 2)(x² + 2x - 15)

Multiply each term in the second factor by each term in the first factor

x(x² + 2x - 15) + 2(x² + 2x - 15) ← distribute both parenthesis

= x³ + 2x² - 15x + 2x² + 4x - 30 ← collect like terms

= x³ + 4x² - 11x - 30

Compare like terms with x³ + ax² - 11x + b

ax² with 4x² ⇒ a = 4

b with - 30 ⇒ b = - 30