Question

If d divides a and d divides b, prove that d divides gcd(a,b).

Answer 1

GCD(a,b) is multiple of d. It means d divides GCD(a,b).

Explanation:

Let a and b are two unknown numbers.

If d divides a and d divides b, then a and b are multiple of d.

`a=d\cdot m=dm`

`b=d\cdot n=dn`

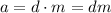
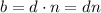
where, m and n are integers.

The greatest common divisor of a and b is

`GCD(a,b)=d\cdot m\cdot n`

`GCD(a,b)=d\cdot mn`

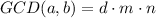
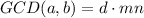
GCD(a,b) is multiple of d. It means d divides GCD(a,b).

Hence proved.