Question

A diffraction grating with 355 lines/mm is 1.2 m in front of a screen. What is the wavelength of light whose first-order maxima will be 16.4 cm from the central maximum on the screen?

Answer 1

The wavelength of light is 381 nm.

Step-by-step explanation:

Given that,

Distance of screen D= 1.2 m

Diffraction grating = 355 lines/mm

Order m= first

Distance from the central maximum on the screen y= 16.5 cm

We need to calculate the width of slits

`d=(1)/(N)`

`d=(1)/(355*10^(-3))`

`d=2.816*10^(-6)\ m`

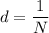
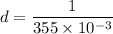
We need to calculate the angle

Using formula of distance

`y=D\tan\theta`

`\thata=\tan^(-1)((y)/(D))`

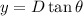
Put the value into the formula

`\theta= \tan^(-1)((0.164)/(1.2))`

`\theta=7.78^(\circ)`

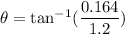
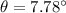
We need to calculate the wave length

Using formula of wavelength

`d\sin\theta=m\lambda`

`\lambda=(d\sin\theta)/(m)`

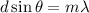
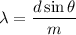
Put the value into the formula

`\lambda=(2.816*10^(-6))/(1)\sin7.78`

`\lambda=381\ nm`

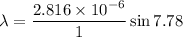
Hence, The wavelength of light is 381 nm.